| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | |||||
| 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 17 | 18 | 19 | 20 | 21 | 22 | 23 |
| 24 | 25 | 26 | 27 | 28 | 29 | 30 |
Tags
- python
- java
- spotify
- 자바
- 회귀
- Baekjoon
- SECS/GEM
- Computer Science
- spring boot
- SW Expert Academy
- C++
- CS
- Gem
- SECS
- MYSQL
- 프로그래머스
- Spring
- modern c++
- SECS-II
- programmers
- c
- 스포티파이
- 회원가입
- linux
- regression
- 파이썬
- Spotify Api
- 백준
- Spring JPA
- SWEA
Archives
- Today
- Total
비버놀로지
[Computer Science] 이진트리 (Binary Tree) 본문
728x90
이진 트리
- 모든 노드들이 2개의 서브트리를 갖는 형태의 트리
- 각 노드가 자식 노드를 최대 2가 가질 수 있음 왼쪽 자식, 오른쪽 자식
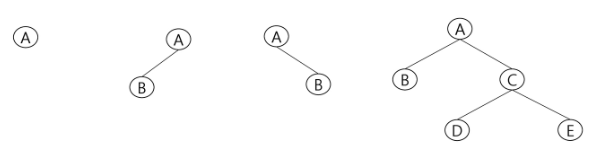
- i 레벨에서 노드의 최대 개수는 2^i 개 (레벨의 노드 개수)
- 높이가 h인 이진트리가 가질 수 있는 노드의 최소 개수는 h+1 개 이며 최대는 2^(h+1)-1 개임 (전체 노드 개수)
포화 이진 트리 (Full Binary Tree)
- 모든 레벨의 노드가 포화상태인 이진 트리
- 높이가 h일때 2^(h+1)-1 개의 노드를 가짐
- 루트를 1번으로 해서 2^(h+1)-1 까지 정해진 노드 번호를 가짐

완전 이진 트리(Complete Binary Tree)
- 높이가 h 이고 노드수가 n일때, 포화 이진 트리의 노드 번호 1번 부터 n번까지 빈자리가 없는 이진 트리
- 순서대로 잘 정렬되있다고 보면됨

편향 이진 트리(Swkewed Binary Tree)
- 높이 h 에 대한 최소의 노드개수를 가지면서 한쪽 방향의 자식노드만 있는 트리
- 왼쪽 편향 이진트리, 오른쪽 편향 이진 트리

이진 트리의 순회
- 전위 순회(pre-order braversal) : VLR
- 부모 - 왼쪽 자식 - 오른쪽 자식 순으로 순회
void preOrderTraversal(TreeNode node) {
if(node != null) {
visit(node);
preOrderTraversal(node.left);
preOrderTraversal(node.right);
}
}
- 중위 순회(in-order braversal) : LVR
- 왼쪽 자식 - 부모 - 오른쪽 자식 순으로 순회
void inOrderTraversal(TreeNode node) { if(node != null) { inOrderTraversal(node.left); visit(node); inOrderTraversal(node.right); } } - 후위 순회(post-order braversal) : LRV
- 왼쪽 자식 - 오른쪽 자식 - 부모 순으로 순회
void postOrderTraversal(TreeNode node) { if(node != null) { postOrderTraversal(node.left); postOrderTraversal(node.right); visit(node); } }
트리의 구현 방법
인접 배열을 이용

루트를 1번으로 하며 레벨n에 있는 노드에 대해 왼쪽부터 2^n ~ 2^(n+1)-1 의 번호를 부여함i 번째 노드의 왼쪽 자식 번호 = i * 2n 레벨의 노드의 시작 번호 2^n배열을 이용한 이진 트리 표현의 단점
- 편향 이진 트리일 경우 메모리 공간의 낭비가 발생
- 트리의 중간에 새로운 노드를 삽입하거나 노드의 삭제가 비효율적임
배열의 최대 크기는 2^(n+1)-1 개를 가짐
i 번째 노드의 오른쪽쪽 자식 번호 = i * 2 +1
i 번째 노드의 부모 번호 = i / 2
인접 리스트의 이용
- ArrayList< ArrayList > list = new ArrayList<>();
728x90
'Computer Science (CS)' 카테고리의 다른 글
| [Computer Science] 레드블랙트리(Red-Black Tree) (0) | 2021.10.14 |
|---|---|
| [Computer Science] 큐(Queue), 덱(Deck) (0) | 2021.09.13 |
| [Computer Science] 트리 (Tree) (0) | 2021.06.28 |
| [Computer Science] 스택 (Stack) (0) | 2021.06.28 |
| [Computer Science] 이중연결리스트 (0) | 2021.06.28 |
Comments




