| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
- 백준
- Computer Science
- modern c++
- CS
- Cars
- Baekjoon
- Spring
- ai이미지변환
- C++
- programmers
- Investing
- spring boot
- 회원가입
- Spring JPA
- 암호화폐투자
- Gem
- finance & economics
- SECS
- SECS-II
- c
- 프로그래머스
- 지브리필터
- Digital Marketing
- SECS/GEM
- 비트코인
- 자바
- 파이썬
- coins
- java
- python
- Today
- Total
비버놀로지
[회귀분석] 다항식 회귀 분석 본문
다항식 회귀 분석
다항식 회귀 분석(Polynomial Linear Regression)은 다중 선형 회귀 분석과 원리가 같습니다. 다만 데이터에 전처리를 함으로써 새로운 변수 간의 조합을 만들어낸 뒤 회귀 분석을 진행하는 것이 차이입니다.
다항식 회귀 분석을 통해 MSE(Mean Squared Error) 값을 원하는 수준까지 맞춰보겠습니다.
MSE
MSE란 평균제곱오차를 의미하며, 통계적 추정에 대한 정확성의 지표로 널리 이용됩니다.
MSE의 수식은 다음과 같습니다.
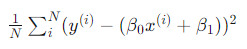
이때 은 데이터의 개수를 의미합니다.
교차 검증
교차 검증이란 모델이 결과를 잘 예측하는지 알아보기 위해 전체 데이터를 트레이닝(training) 세트와 테스트(Test) 세트로 나누어 모델에 넣고 성능을 평가하는 방법입니다. 트레이닝 데이터는 모델을 학습시킬 때 사용되고, 테스트 데이터는 학습된 모델을 검증할 때 사용됩니다.
sklearn의 model_selection 에서 데이터 세트를 나눠주는 기능을 제공합니다. 실습의 맨 위 부분에서 해당 모듈을 추가합니다.
from sklearn.model_selection import train_test_splitx_train, x_test, y_train, y_test = train_test_split(X_poly, Y, test_size=0.2, random_state=0)위 코드의 의미는 데이터의 80%를 모델 트레이닝에 사용하고, 나머지 20%를 모델 검증에 사용한다는 의미입니다.
random_state는 트레이닝과 테스트 데이터 그룹을 나눌 때 사용되는 난수 시드입니다. 이 값을 변경하여 트레이닝과 테스트 세트를 임의의 다른 값으로 초기화할 수 있습니다.
과적합
모델을 복잡하게 만들면 트레이닝 데이터에 대한 정확도를 높일 수 있지만, 동일한 모델을 테스트 데이터에 적용하면 과적합(Overfitting) 현상이 일어나게 됩니다.
과적합 현상은 트레이닝 데이터에만 적합하게끔 모델이 작성되어, 테스트 데이터 또는 실제 데이터에 대해 모델이 잘 적용되지 않는 현상입니다.
실습
- 주어진 코드를 살펴보세요. 스켈레톤 코드는 다음 모델을 구현한 것입니다.

주어진 모델에서 변수의 조합을 더하거나 빼면서 MSE의 값을 최대한 낮춰보세요.
3. 테스트 데이터에서의 MSE를 1 미만으로 만들어보세요. 모델을 복잡하게 만들 경우 과적합이 일어나는 점을 주의하세요.
import numpy as np
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
from sklearn.model_selection import train_test_split
'''
./data/Advertising.csv 에서 데이터를 읽어, X와 Y를 만듭니다.
X는 (200, 3) 의 shape을 가진 2차원 np.array,
Y는 (200,) 의 shape을 가진 1차원 np.array여야 합니다.
X는 FB, TV, Newspaper column 에 해당하는 데이터를 저장해야 합니다.
Y는 Sales column 에 해당하는 데이터를 저장해야 합니다.
'''
import csv
csvreader = csv.reader(open("data/Advertising.csv"))
x = []
y = []
next(csvreader)
for line in csvreader :
x_i = [ float(line[1]), float(line[2]), float(line[3]) ]
y_i = float(line[4])
x.append(x_i)
y.append(y_i)
X = np.array(x)
Y = np.array(y)
# 다항식 회귀분석을 진행하기 위해 변수들을 조합합니다.
X_poly = []
for x_i in X:
X_poly.append([
# x_i[0] ** 2, # X_1^2
# x_i[1], # X_2
# x_i[1] * x_i[2], # X_2 * X_3
# x_i[2] # X_3
x_i[0], # X_1^2
x_i[1], # X_2
x_i[0] * x_i[1],
x_i[0] * x_i[1] * x_i[2],
x_i[0]**2
])
# X, Y를 80:20으로 나눕니다. 80%는 트레이닝 데이터, 20%는 테스트 데이터입니다.
x_train, x_test, y_train, y_test = train_test_split(X_poly, Y, test_size=0.2, random_state=0)
# x_train, y_train에 대해 다항식 회귀분석을 진행합니다.
lrmodel = LinearRegression()
lrmodel.fit(x_train, y_train)
#x_train에 대해, 만든 회귀모델의 예측값을 구하고, 이 값과 y_train 의 차이를 이용해 MSE를 구합니다.
predicted_y_train = lrmodel.predict(x_train)
mse_train = mean_squared_error(y_train, predicted_y_train)
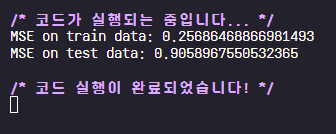
print("MSE on train data: {}".format(mse_train))
# x_test에 대해, 만든 회귀모델의 예측값을 구하고, 이 값과 y_test 의 차이를 이용해 MSE를 구합니다. 이 값이 1 미만이 되도록 모델을 구성해 봅니다.
predicted_y_test = lrmodel.predict(x_test)
mse_test = mean_squared_error(y_test, predicted_y_test)
print("MSE on test data: {}".format(mse_test))
'인공지능 머신러닝' 카테고리의 다른 글
| [나이브 베이즈 분류] 확률로 pi 계산하기 (0) | 2022.11.03 |
|---|---|
| [회귀분석] 영어 단어 코퍼스 분석하기 (0) | 2022.11.03 |
| [회귀분석] 다중 회귀 분석 (0) | 2022.11.03 |
| [회귀분석] Scikit-learn을 이용한 회귀분석 (0) | 2022.11.03 |
| [회귀분석] Loss Function (0) | 2022.11.03 |




