| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 |
Tags
- 비트겟
- Gem
- Spring
- 파이썬
- Baekjoon
- spotify
- 자바
- SECS/GEM
- SECS-II
- 회귀
- java
- MYSQL
- modern c++
- SW Expert Academy
- C++
- spring boot
- regression
- SECS
- Spring JPA
- 회원가입
- Computer Science
- Spotify Api
- c
- python
- 스포티파이
- SWEA
- 백준
- 프로그래머스
- programmers
- CS
Archives
- Today
- Total
비버놀로지
[회귀(Regression)] 회귀 분석(Regression)알고리즘 구현하기 본문
728x90
회귀 분석(Regression) 알고리즘 구현하기
이번 실습에서는 간단한 파이썬 코드 작성을 통해 회귀 분석 알고리즘을 구현해보도록 하겠습니다.
이론 강의를 통해 회귀 모델은 다음과 같이 표현한다고 하였습니다.
Y=β0+β1X
여기서 적절한 β0 와 β1 를 찾기 위해서는 데이터의 실제 값과 모델이 예측하는 값의 차이를 최소한으로 하는 선을 찾아야 합니다.
차이를 최소한으로 하는 선을 찾는 회귀 분석의 절차는 다음과 같습니다.
회귀 분석의 절차
- X라는 값이 입력되면 Y=β0+β1X라는 계산식을 통해 값을 산출하는 예측 함수를 정의합니다.
- 실제 값 y와 예측 함수를 통해 도출된 예측값 pred_y간의 차이를 계산합니다.
- 계산한 차이에 기반하여 β0와 β1를 업데이트하는 규칙을 정의하고 이를 바탕으로 β0와 β1의 값을 조정합니다.
- 위의 과정을 특정 반복 횟수(iteration) 만큼 반복합니다.
- 반복적으로 수정된 β0와 β1를 바탕으로 Y=β0+β1X라는 회귀식을 정의합니다.
실습
- beta_0, beta_1, X 를 받아서 예측값 y_pred를 계산하여 반환하는 prediction() 함수를 구현합니다.
- 반복 횟수만큼 오차(loss)를 계산하고 beta_0,beta_1의 값을 변경하는 함수인 gradient_descent() 를 구현합니다.
- 실행 버튼을 눌러 회귀 분석 과정의 시각화를 확인합니다.
- 제출 버튼을 눌러 올바른 회귀 알고리즘 구현 여부를 확인합니다.
Tips!
- 현재 실습 해설 영상의 update_beta() 함수에 대한 설명(6:17~8:50)에서 delta_0와 delta_1에 대한 설명이 바뀌어있습니다. 우측에 올바른 코드가 주어져 있는 점 참고 부탁드립니다.
- gradient_descent() 함수 내 loss의 정의가 영상에서는 단순히 실제 y와 예측한 y의 차이로 되어 있는데, 실제 선형 회귀에서는 MSE를 loss 함수로 사용합니다. 이에 따라 코드도 MSE를 사용한 것으로 변경하였으니 참고 부탁드립니다.
import numpy as np
import matplotlib.pyplot as plt
from elice_utils import EliceUtils
elice_utils = EliceUtils()
# 데이터를 생성하고 반환하는 함수입니다.
def load_data():
X = np.array([[8.70153760], [3.90825773], [1.89362433], [3.28730045], [7.39333004], [2.98984649], [2.25757240], [9.84450732], [9.94589513], [5.48321616]])
y = np.array([[5.64413093], [3.75876583], [3.87233310], [4.40990425], [6.43845020], [4.02827829], [2.26105955], [7.15768995], [6.29097441], [5.19692852]])
return X, y
"""
1. 입력값(X)과 beta_0,beta_1를 바탕으로
예측값(pre_y)을 계산하여 반환하는 함수를 구현합니다.
회귀 함수 식을 참고하여
예측값을 계산합니다.
"""
def prediction(beta_0, beta_1, X):
y_pred = beta_0 + beta_1 * X
return y_pred
# beta_1와 beta_1 값을 업데이트 하는 규칙을 정의하는 함수입니다.
def update_beta(X, y, y_pred, lr):
delta_0 = -(lr * (2 / len(X)) * np.sum(y - y_pred))
delta_1 = -(lr * (2 / len(X)) * (np.dot(X.T, (y - y_pred))))
return delta_0, delta_1
"""
2. 반복 횟수만큼 오차(loss)를 계산하고
beta_0,beta_1의 값을 변경하는 함수를 구현합니다.
Step01. 실제 값 y와 prediction 함수를 통해 예측한
예측 값 pred_y 간의 차이(loss)를 계산합니다.
loss는 실제값(y) - 예측값(pred_y)으로 정의하겠습니다.
Step02. 구현된 함수를 이용하여
beta_0와 beta_1 의 변화값을 각각 beta0_delta, beta1_delta에 저장합니다.
"""
def gradient_descent(X, y, iters, lr):
beta_0 = np.zeros((1,1))
beta_1 = np.zeros((1,1))
for i in range(iters):
y_pred = prediction(beta_0, beta_1, X)
loss = np.mean(np.square(y - y_pred))
beta0_delta, beta1_delta = update_beta(X, y, y_pred, lr)
beta_0 -= beta0_delta
beta_1 -= beta1_delta
# 100번의 학습마다 그래프 출력하기
if i%100==0:
print("학습 횟수 :",i)
plotting_graph(X,y,beta_0,beta_1)
return beta_0, beta_1
# 그래프를 시각화하는 함수입니다.
def plotting_graph(X,y,beta_0,beta_1):
y_pred = beta_0 + beta_1[0,0] * X
fig = plt.figure()
plt.scatter(X, y)
plt.plot(X, y_pred,c='r')
plt.savefig("test.png")
elice_utils.send_image("test.png")
# 회귀 알고리즘 구현 진행을 위한 main() 함수입니다.
def main():
# 학습을 위해 필요한 파라미터입니다.
lr = 1e-4
iteration = 1000
X, y = load_data()
beta_0, beta_1 = gradient_descent(X, y, iteration, lr)
print("{}번의 학습 이후의 회귀 알고리즘 결과".format(iteration))
print("beta_0:",beta_0[0], "beta_1:",beta_1[0])
plotting_graph(X,y,beta_0,beta_1)
return beta_0, beta_1
if __name__=="__main__":
main()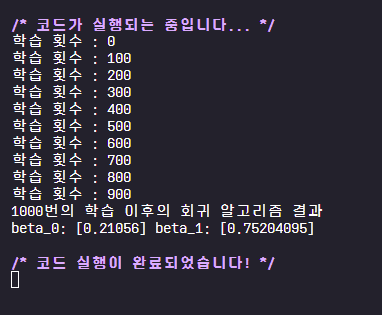

728x90
'인공지능 머신러닝' 카테고리의 다른 글
| [회귀(Regression)] 다중 선형 회귀 모델 구현하기 (0) | 2022.11.06 |
|---|---|
| [회귀(Regression)] 단순 선형 회귀 모델 구현하기 (0) | 2022.11.06 |
| [K-Means 클러스터링] 이미지 색상 수 줄이기 (0) | 2022.11.04 |
| [K-Means 클러스터링] K-Means 클러스터링 (0) | 2022.11.04 |
| [K-Means 클러스터링] PCA 차원축소 (0) | 2022.11.04 |
Comments




