| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
- python
- Gem
- 회원가입
- finance & economics
- 프로그래머스
- Digital Marketing
- 암호화폐투자
- 비트코인
- modern c++
- 자바
- Computer Science
- Cars
- java
- ai이미지변환
- programmers
- Investing
- Spring JPA
- CS
- Baekjoon
- Spring
- SECS/GEM
- SECS
- coins
- c
- spring boot
- 지브리필터
- 백준
- SECS-II
- 파이썬
- C++
- Today
- Total
비버놀로지
[BAEKJOON 백준] 11660 구간 합 구하기 5 (JAVA) 본문
https://www.acmicpc.net/problem/11660
11660번: 구간 합 구하기 5
첫째 줄에 표의 크기 N과 합을 구해야 하는 횟수 M이 주어진다. (1 ≤ N ≤ 1024, 1 ≤ M ≤ 100,000) 둘째 줄부터 N개의 줄에는 표에 채워져 있는 수가 1행부터 차례대로 주어진다. 다음 M개의 줄에는 네
www.acmicpc.net
문제
N×N개의 수가 N×N 크기의 표에 채워져 있다. (x1, y1)부터 (x2, y2)까지 합을 구하는 프로그램을 작성하시오. (x, y)는 x행 y열을 의미한다.
예를 들어, N = 4이고, 표가 아래와 같이 채워져 있는 경우를 살펴보자.
| 1 | 2 | 3 | 4 |
| 2 | 3 | 4 | 5 |
| 3 | 4 | 5 | 6 |
| 4 | 5 | 6 | 7 |
여기서 (2, 2)부터 (3, 4)까지 합을 구하면 3+4+5+4+5+6 = 27이고, (4, 4)부터 (4, 4)까지 합을 구하면 7이다.
표에 채워져 있는 수와 합을 구하는 연산이 주어졌을 때, 이를 처리하는 프로그램을 작성하시오.
입력
첫째 줄에 표의 크기 N과 합을 구해야 하는 횟수 M이 주어진다. (1 ≤ N ≤ 1024, 1 ≤ M ≤ 100,000) 둘째 줄부터 N개의 줄에는 표에 채워져 있는 수가 1행부터 차례대로 주어진다. 다음 M개의 줄에는 네 개의 정수 x1, y1, x2, y2 가 주어지며, (x1, y1)부터 (x2, y2)의 합을 구해 출력해야 한다. 표에 채워져 있는 수는 1,000보다 작거나 같은 자연수이다. (x1 ≤ x2, y1 ≤ y2)
출력
총 M줄에 걸쳐 (x1, y1)부터 (x2, y2)까지 합을 구해 출력한다.
1) 어떻게 풀 것인가?
N이 1024이고, 부분합을 M(100,000) 번 구해야한다.
단순하게 그때 그때 부분합을 구하게 되면 N^2(1024*1024) * M(10만)으로 시간초과가 예상된다.
문제는 크게 ① DP[ i ][ j ] 누적합을 만드는 점화식과 ② 문제에서 질문한 넓이를 구하는 점화식으로 나뉘어진다.
① DP[ i ][ j ] 누적합을 만드는 점화식
// (위에↑ 값) + (왼쪽← 값) - (↖중복되는 대각선 값) + (인풋값)
dp[i][j] = dp[i - 1][j] + dp[i][j - 1] - dp[i - 1][j - 1] + map[i][j];
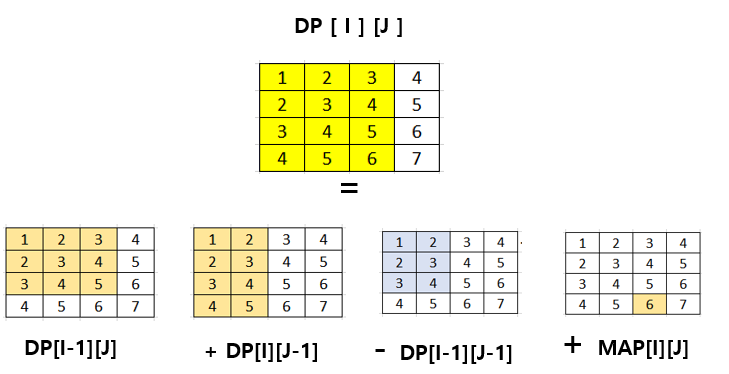
DP[ i ][ j ] 를 1,1 부터 i, j까지의 합이라고 가정한다면 쉽게 풀 수 있는 DP문제이다.
② 문제에서 질문한 넓이를 구하는 점화식
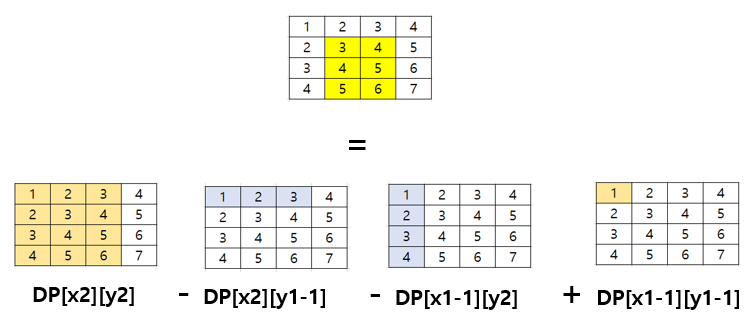
점화식은 이 그림으로 요약할 수 있다.
2) 시간복잡도
N^2번 입력 받을떄 누적합을 구하므로 O(N^2) - N은 1,024로 양호함
(Java 기준 - 944ms)
3) 공간복잡도
2차원 배열로 N이 크지 않으므로(1024^2) 특별히 고려하지 않음.
4) 풀면서 놓쳤던점
x = j / y = i 라고 착각했는데, 예제가 틀리길래 확인해보니, x가 i / y가 j 였다.
일반적인 좌표평면과 달라 주의.
5) 이 문제를 통해 얻어갈 것
DP적 사고방식. 부분의 정답을 모아 전체의 정답을 만들기 - 2차원 버전
예제 입력 1 복사
4 3
1 2 3 4
2 3 4 5
3 4 5 6
4 5 6 7
2 2 3 4
3 4 3 4
1 1 4 4
예제 출력 1 복사
27
6
64
예제 입력 2 복사
2 4
1 2
3 4
1 1 1 1
1 2 1 2
2 1 2 1
2 2 2 2
예제 출력 2 복사
1
2
3
4
DP를 활용을 해서 누적합을 구한 뒤 결과값을 출력하도록 했다.
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int N = Integer.parseInt(st.nextToken());
int M = Integer.parseInt(st.nextToken());
int map[][] = new int[N + 1][N + 1];
int dp[][] = new int[N + 1][N + 1];
int sum[] = new int[M];
for (int i = 1; i <= N; i++) {
st = new StringTokenizer(br.readLine());
for (int j = 1; j <= N; j++) {
map[i][j] = Integer.parseInt(st.nextToken());
}
}
for (int i = 1; i <= N; i++) {
for (int j = 1; j <= N; j++) {
dp[i][j] = dp[i - 1][j] + dp[i][j - 1] - dp[i - 1][j - 1] + map[i][j];
}
}
for (int i = 0; i < M; i++) {
st = new StringTokenizer(br.readLine());
int x1 = Integer.parseInt(st.nextToken());
int y1 = Integer.parseInt(st.nextToken());
int x2 = Integer.parseInt(st.nextToken());
int y2 = Integer.parseInt(st.nextToken());
sum[i] += dp[x2][y2] - dp[x2][y1 - 1] - dp[x1 - 1][y2] + dp[x1 - 1][y1 - 1];
System.out.println(sum[i]);
}
}
}
'ALGORITM > JAVA' 카테고리의 다른 글
| [BAEKJOON 백준] 9935 문자열 폭발 (JAVA) (0) | 2022.05.05 |
|---|---|
| [BAEKJOON 백준] 3020 개똥벌레 (JAVA) (0) | 2022.05.05 |
| [BAEKJOON 백준] 16235 나무 재테크 (JAVA) (0) | 2022.04.30 |
| [BAEKJOON 백준] 15684 사다리 조작 (JAVA) (0) | 2022.04.30 |
| [BAEKJOON 백준] 17822 원판 돌리기 (JAVA) (0) | 2022.04.29 |


