| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 |
Tags
- regression
- 회원가입
- C++
- Baekjoon
- Spring JPA
- Computer Science
- 백준
- spotify
- 회귀
- 비트겟
- SECS-II
- SW Expert Academy
- java
- programmers
- spring boot
- 파이썬
- 스포티파이
- c
- python
- Spring
- SECS/GEM
- 프로그래머스
- SECS
- modern c++
- SWEA
- Gem
- MYSQL
- Spotify Api
- 자바
- CS
Archives
- Today
- Total
비버놀로지
[선형대수학 Numpy] 벡터 연산으로 그림 그리기 본문
728x90
벡터 연산으로 그림 그리기
이번 미션에서는 Numpy를 이용한 벡터 연산으로 원과 다이아몬드 그림을 그리고, 이것들을 조합해 smile 그림을 그려보겠습니다.
캔버스
그림을 그리기 위해서는 그림을 그릴 공간이 필요합니다. 이 프로젝트에서는 이 공간을 xrange, yrange 라는 변수로 지정하겠습니다.
만약,
xrange = [1, 3]
yrange = [2, 4]라면, 그림을 그릴 캔버스는 (1,2)(1, 2), (3,4)(3, 4) 로 지정된 공간을 사용하게 됩니다.
그림 그리기
그림을 그리기 위해서, 다음 방식을 사용하겠습니다. 어떤 함수 f와 매우 작은 숫자 threshold에 대해,
- 캔버스 내에 점 P = (x, y)을 임의로 생성한다.
- f(P) < threshold 라면 점을 찍는다. 만약 그렇지 않다면, 점을 찍지 않는다.
- 이것을 100,000 회 반복한다.
왜 f(P) == 0 일 때 점을 찍지 않고, 아주 작은 값 threshold 보다 작을 때 점을 찍는지, 한번 생각해 보세요!
원 그리기
(0,0)(0, 0) 이 중심이고, 반지름 1인 원의 방정식은 다음과 같습니다.
x2+y2=1x^2 + y^2 = 1
원의 그림을 그리는 방식을 생각하면, 정확히 원 위에 있는 점들에 대해서 circle(P) 는 0을 가져야 합니다. 그러므로, circle(P) 는 다음과 같이 정의할 수 있습니다.
x = P[0]
y = P[1]
return sqrt(x ** 2 + y ** 2) - 1위 코드의 리턴값은 수업시간에 배운 것과 같이 다음과 같습니다.
return sqrt(np.sum(P * P)) - 1Norm의 개념을 사용한다면 다음과도 같습니다.
return np.linalg.norm(P) - 1다이아몬드 그리기
(0,0)(0, 0) 이 중심이고, 원점에서 각 꼭지점까지 이르는 거리가 1인 다이아몬드의 방정식은 다음과 같습니다.
∣x∣+∣y∣=1|x| + |y| = 1
원 그리기와 같은 방식으로 생각해본다면, right_eye(P)는 다음과 같이 정의할 수 있습니다.
return np.abs(P[0]) + np.abs(P[1]) - 1실습
- circle함수의 구성을 확인해보세요.
- diamond함수의 구성을 확인해보세요.
- smile함수의 구성을 확인해보세요. 어떻게
- 동작하는지 한 번 생각해보세요.
- sample함수의 구성을 확인해보고, 53번째 줄의 변수들을 바꿔보면서 실행해보세요. 결과가 어떻게 달라지나요?
import matplotlib as mpl
mpl.use("Agg")
import matplotlib.pyplot as plt
import elice_utils
import numpy as np
elice = elice_utils.EliceUtils()
def circle(P):
return np.linalg.norm(P) - 1 # 밑의 코드와 동일하게 동작합니다.
# return np.sqrt(np.sum(P * P)) - 1
def diamond(P):
return np.abs(P[0]) + np.abs(P[1]) - 1
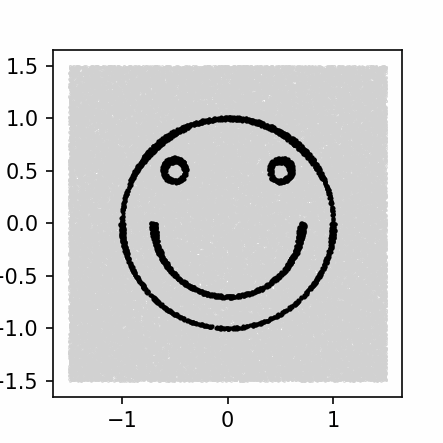
def smile(P):
def left_eye(P):
eye_pos = P - np.array([-0.5, 0.5])
return np.sqrt(np.sum(eye_pos * eye_pos)) - 0.1
def right_eye(P):
eye_pos = P - np.array([0.5, 0.5])
return np.sqrt(np.sum(eye_pos * eye_pos)) - 0.1
def mouth(P):
if P[1] < 0:
return np.sqrt(np.sum(P * P)) - 0.7
else:
return 1
return circle(P) * left_eye(P) * right_eye(P) * mouth(P)
def checker(P, shape, tolerance):
return abs(shape(P)) < tolerance
def sample(num_points, xrange, yrange, shape, tolerance):
accepted_points = []
rejected_points = []
for i in range(num_points):
x = np.random.random() * (xrange[1] - xrange[0]) + xrange[0]
y = np.random.random() * (yrange[1] - yrange[0]) + yrange[0]
P = np.array([x, y])
if (checker(P, shape, tolerance)):
accepted_points.append(P)
else:
rejected_points.append(P)
return np.array(accepted_points), np.array(rejected_points)
xrange = [-1.5, 1.5] # X축 범위입니다.
yrange = [-1.5, 1.5] # Y축 범위입니다.
accepted_points, rejected_points = sample(
100000, # 점의 개수를 줄이거나 늘려서 실행해 보세요. 너무 많이 늘리면 시간이 오래 걸리는 것에 주의합니다.
xrange,
yrange,
smile, # smile을 circle 이나 diamond 로 바꿔서 실행해 보세요.
0.005) # Threshold를 0.01이나 0.0001 같은 다른 값으로 변경해 보세요.
plt.figure(figsize=(xrange[1] - xrange[0], yrange[1] - yrange[0]),
dpi=150) # 그림이 제대로 로드되지 않는다면 DPI를 줄여보세요.
plt.scatter(rejected_points[:, 0], rejected_points[:, 1], c='lightgray', s=0.1)
plt.scatter(accepted_points[:, 0], accepted_points[:, 1], c='black', s=1)
plt.savefig("graph.png")
elice.send_image("graph.png")
728x90
'인공지능 머신러닝' 카테고리의 다른 글
| [회귀분석] Loss Function (0) | 2022.11.03 |
|---|---|
| [회귀분석] 기울기와 절편 (0) | 2022.11.03 |
| [선형대수학 Numpy] Numpy 논리연산자 (0) | 2022.11.03 |
| [선형대수학 Numpy] Numpy 산술연산자 (0) | 2022.11.03 |
| [선형대수학 Numpy] Numpy 행렬 (0) | 2022.11.03 |
Comments





