| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 |
- linux
- spring boot
- SECS
- 파이썬
- CS
- SW Expert Academy
- java
- spotify
- Computer Science
- modern c++
- 백준
- Spotify Api
- SWEA
- 회귀
- SECS/GEM
- Spring
- 스포티파이
- C++
- regression
- MYSQL
- 자바
- Baekjoon
- Spring JPA
- python
- Gem
- 프로그래머스
- programmers
- SECS-II
- c
- 회원가입
- Today
- Total
비버놀로지
[Computer Science] 레드블랙트리(Red-Black Tree) 본문
AVL트리
-불균형 상태
- 일반적인 이진검색트리는 트리구조가 한쪽으로 치우쳐지는 경우가 있다. 이진검색트리의 검색성능은 높이에 의해 결정된다 → 한 쪽으로 치우치지않고 양쪽 균형을 맞추자!
- 하나의 노드를 기준으로 양쪽 서브트리의 높이 차이가 2 이상인 경우
- balance factor : bf ( 왼쪽서브트리높이 - 오른쪽 서브트리의 높이) 가 절댓값 2 이사이면 불균형
- 불균형 상태가 되면 리밸런싱 작업을 수행한다. ( 회전을 통해 )

- 여기에 15를 삽입해보자

→→현재 14의 높이는 2 , NIL의 높이는 0이므로 불균형 상태가 되었다.
-회전
- 회전의 종류에는 1번만 회전하는 LL, RR 2번 회전시키는 LR,RL이 존재한다.
1. LL회전

-LL일때는 트리를 오른쪽으로 회전시켜주면 된다.
2. RR회전

- RR일 때는 왼쪽으로 트리를 회전시키면 된다.
3. LR회전

- 마지막 노드인 422값을 부모노드와 자리를 바꾸면 바로 LL형태가 된다 → LL회전한번더
4. RL회전

- 마지막 노드인 422값을 부모노드와 자리를 바꾸면 바로 RR형태가 된다 → RR회전한번더
AVL트리의 장단점
장점
검색, 삽입, 삭제 모두 O(log N)이며 항상 균형을 맞춘다.
단점
프로그래밍하기 어렵고 디버깅또한 어렵다. 검색, 삽입, 삭제가 빠르긴 하지만 균형을 맞추는데 필요한 연산이 많다.
Red-Black Tree
- 이진탐색트리의 일종
- 균형잡힌 트리 : 높이가 O(logN)
- SEARCH, INSERT, DELETE 연산을 최악의 경우에도 O(logN)시간에 지원
C++의 map이 레드 블랙 트리 기반이다.
- 설명
레드블랙트리는 이진탐색트리를 확장시켜서 균형기능을 추가시킨 트리입니다.
여기서 균형을 지키기 위한 조건이 5가지 있는데
이 조건을 만족하게 된다면 최악의 경우에도 가장 먼 거리가 가장 가까운 경로까지의 거리의 2배보다 항상 작게 됩니다.
따라서 균형잡힌 이진탐색트리가 되어 삽입, 삭제, 검색시에 최악의 경우에도 일정한 실행시간 O(log n)을 보장할 수 있습니다.
쓰이는 예로는, c++ stl의 map에서 red black트리가 쓰입니다.
balanced binary search tree 대표적인 예 : AVL트리, 레드블랙트리
레드 블랙 트리는 balanced binary search tree로

이와 같은 모양이 나오지 않도록 "조건"을 걸어놈

레드블랙트리 조건
- 모든 노드는 레드, 블랙이다.
- 루트노드의 색깔은 검정이다
- 모든 리프노드는 NIL이고 검정이다.
- 노드가 레드이면 그 노드의 자식은 반드시 검정이다. ( No Double Red )
- 루트 노드에서 임의의 리프 노드에 이르는 경로에서 만나는 블랙 노드의 수는 모두 같다.
NIL 노드 : 자식 노드가 존재하지 않을 경우 NIL 노드라고 부르는 특수한 노드가 있다고 가정
왼쪽 자식과 오른쪽 자식이 없다고 하지않고 NIL노드를 자식으로 가지고 있다고 표현
루트의 부모도 NIL노드라고 가정
→ 실제 구현 시에 쓰이는 것이 아니고, 설명의 간편성을 위해 가상의 노드가 있다고 가정한 것
삽입

1번 조건에 의해 루트노드의 색깔은 검정을 줬음
이제 값들을 삽입하는데, 삽입되는 노드의 색깔은 무조건 Red


이때 3번 조건을 위반함 Double Red
Double Red를 해결하는 전략 2가지가 있다.

z가 삽입노드이고 w가 삼촌노드이다.
w가 검정일때 Restructuring, w가 빨강일때 Recoloring을 수행
- Restructuring
- 나와 내 부모, 부모의 부모를 오름차순으로 정렬
- 무조건 가운데 있는 값을 부모로 만들고 나머지 둘을 자식으로 만든다.
- 올라간 가운데 있는 값을 검정으로 만들고 그 두자식들을 빨강으로 만든다.
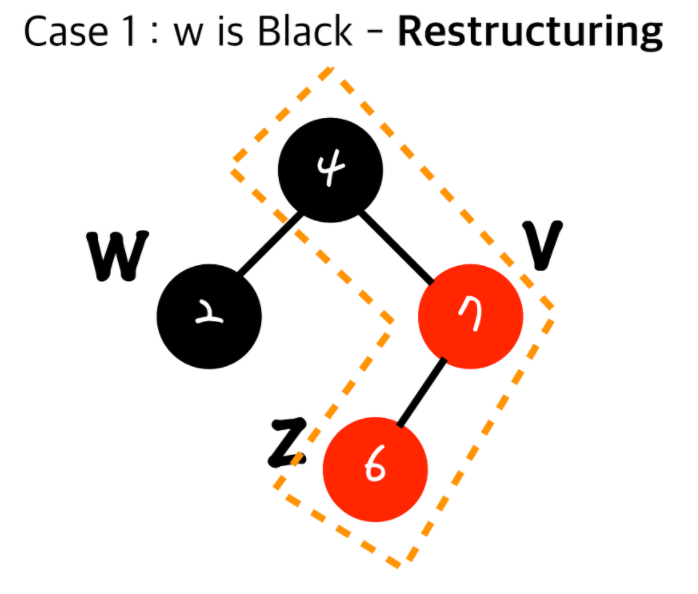

오름차순 정렬

가운데 있는 값 부모로 만들고

부모로 올라간 값은 검정, 나머지 자식은 빨강으로 만든다.

원래 4의 자식이었던 2를 추가
Restructuring은 다른 서브트리에 영향을 끼치지 않기 때문에 한번의 Restructuring이면 끝남.
여기서 말하는 영향은 4번 조건인 경로상의 검정 노드의 수이다.
Double Red를 해결하기 전과 후의 검정 노드의 개수에 변화가 없기 때문에 다른 서브트리에 영향을 끼치지 않음
Restructuring자체의 시간복잡도는 O(1)에 끝나지만, (순서결정시간 - 상수시간, 트리로 만드는시간 - 상수시간, 원래있던 노드들의 구조들을 바꿔주는 시간 - 상수시간)
Restructuring은 어떤 노드를 insertion한 뒤 일어나므로 총 수행시간은 **O(logn)**이에요. 지금 현재 노드가 들어갈 위치를 먼저 찾아야 하기 때문이죠.
- Recoloring
- 현재 insert된 노드(z)의 부모와 그 형제(w)를 검정(Black)으로 하고 부모의 부모를 빨강으로 한다.
- 부모의 부모가 Root node가 아니었을 시 Double Red가 다시 발생 할 수 있다.


여기서 4가 Root Node 였다면 1번 조건에 의해 검정이 된다.
하지만 어떤 큰 트리의 서브트리라고 한다면 4라는 key를 가진 노드의 부모가 또 빨강일 수 있다.
레드블랙트리에 삽입(insertion)하는경우, Restructuring을 하든, Recoloring을 하든 O(logn)이 걸리게됩니다.
삭제
삭제시 주의할 점은 삭제로 인해 4번 조건인 루트에서 리프노드까지 경로의 검정 노드의 수가 모두 같다라는 조건이 위배되는 것이다.
- 기본 케이스
m을 삭제한다고 했을 때

- m이 레드인 경우는 그냥 삭제
- m이 블랙이고 자식이 레드인 경우는 삭제후 x의 노드를 블랙으로 바꾸면된다.
- 까다로운 경우

m과 x가 둘다 블랙인 경우 m을 삭제하면 블랙노드의 개수가 1개 줄기 때문에
레드블랙트리 조건 4번에 위반하게 된다.

Case 1-1
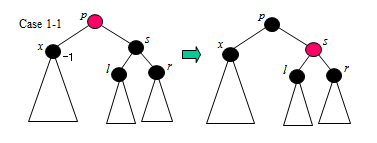
p와 s의 색상을 맞바꾼다.
Case *-2

p를 중심으로 왼쪽으로 회전시키고, p와 s의 색상을 바꾼 다음 r의 색상을 레드에서 블랙으로 바꾼다
Case *-3

s를 중심으로 오른쪽으로 회전시키고 l과 s의 색상을 맞바꾼다. Case *-2로 이동한다.
Case 2-1
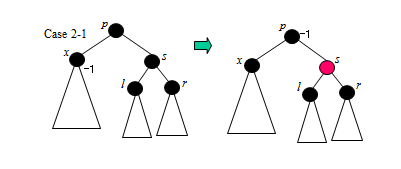
단순히 s의 색상을 블랙에서 레드로 바꾼다. 이제 s를 지나가는 경로에서도 블랙 노드가 하나 모자라게 되어 p를 지나가는 경로 전체에서 블랙 노드가 하나 모자라게 된다. 이것은 원래 x에 대해서 발생했던 문제와 똑같은 문제가 p에 대해서 발생했음을 뜻한다. 재귀적으로 이 문제를 해결한다.
Case 2-4

p를 중심으로 왼쪽으로 회전시키고 p와 s의 색상을 맞바꾼다. l과 r을 경유하는 경로와 관련해서는 문제가 없다. 다만 문제가 발생한 x의 부모 노드의 색상이 블랙에서 레드로 바뀌었다. 이것은 Case 1에 해당하므로 Case 1로 이동한다.
https://itstory.tk/entry/레드블랙-트리Red-black-tree
Red-Black vs AVL
- AVL트리는 더욱 엄격한 균형을 이루고 있기 때문에 Red-Black 트리보다 더 빠른 조회를 제공
- Red-Black 트리는 상대적으로 느슨한 균형으로 인해 회전이 거의 이루어지지 않기 때문에 AVL트리보다 빠르게 삽입 및 제거 작업을 수행
- AVL트리는 각 노드에 대해 BF를 저장하므로 노드 당 int 저장이 필요Red-Black 트리는 노드당 1비트의 정보만 필요합니다. (플래그 반전만 시키면 됨)
- Red-Black 트리는 맵, C++의 멀티캐스트, Java treeMap 등 대부분의 언어 라이브러리에서 사용, AVL트리는 더 빠른 검색이 필요한 데이터베이스에서 사용
'Computer Science (CS)' 카테고리의 다른 글
| [Computer Science] 힙(Heap) (0) | 2021.10.14 |
|---|---|
| [Computer Science] B-트리(B-Tree) (0) | 2021.10.14 |
| [Computer Science] 큐(Queue), 덱(Deck) (0) | 2021.09.13 |
| [Computer Science] 이진트리 (Binary Tree) (0) | 2021.06.28 |
| [Computer Science] 트리 (Tree) (0) | 2021.06.28 |




