B-Tree
B-Tree는 ORACLE과 같은 상용 DB에서 많이 사용하는 자료구조이며 외부검색에 유용하다고 알려짐, 이진 트리를 확장한 구조이다.
특성
- M차 B-Tree의 높이는 $log_{m/2}N$ 즉, O(logN)의 성능
- 한 노드에 M개의 자료, M+1개의 자식을 가질 수 있음
- 외부검색에 적합
- 하나의 노드크기를 Disk I/O 단위의 크기로
하나의 노드가 다량의 데이터를 가질수 있기에 입출력시에 불러오는 블럭의 크기만큼 노드의 크기를 설정한다면 외부기억장치에 접근하는 횟수가 줄어들기 때문에 데이터를 빠르게 처리할 수 있다.
https://www.cs.usfca.edu/~galles/visualization/BTree.html
이진 트리의 한계 : 두 개의 자식밖에 가지질 못하고 자칫 균형이 맞지 않으면 검색 효율이 선형검색 급
편향 트리
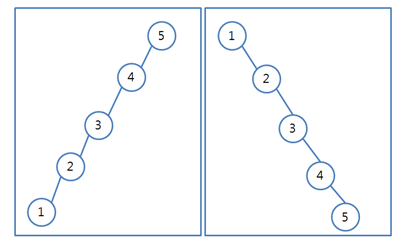
탐색, 삽입, 삭제
시간복잡도
O(h), h는 트리의 높이 → 최악의 경우 O(n)
편향 트리와 같은 밸런스가 맞지 않은 트리를 Unbalanced Tree라고 합니다.
반대로 완전 이진 트리와 같은 균형이 잡힌 트리를 Balanced Tree라고 하죠.
B-Tree는 이러한 방법 중 하나
B-Tree 규칙
- 노드의 자료수가 N이라면, 자식의 수는 N+1 이어야 한다.
- 각 노드의 자료는 정렬된 상태여야 한다.
- D노드의 왼쪽 서브트리는 D보다 작은 값들이고 D의 오른쪽 서브트리는 D보다 큰 값들이다.
- Root노드는 적어도 2개이상의 자식을 가져야 한다. (Root 혼자 있을때는 상관없음)
- Root노드를 제외한 모든 노드는 적어도 M/2개의 자료를 가지고 있어야 한다.
- 외부노드로 가는 경로의 길이는 모두 같다. ( balanced tree )
- 입력자료는 중복될 수 없다.
삽입
- 자료는 항상 Leaf 노드에 추가된다.
- 리프 노드의 선택은 ROOT 노드부터 시작해 하향식으로 탐색하며 결정한다.
- 추가될 Leaf 노드에 여유가 있다면 그냥 삽입, 없다면(overflow) 분할
3차 B트리
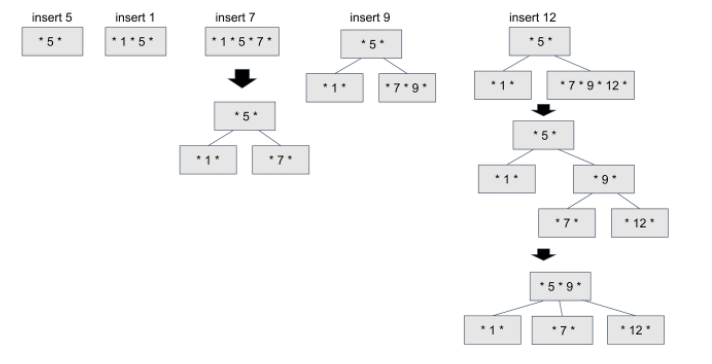
overflow 발생 시 노드의 중앙값을 부모로 올리고 두개의 노드로 분리
삭제
1-1. 리프노드에서 삭제시 바로 삭제
1-2. 중간노드에서 삭제시 자기보다 작은값의 자식노드와 자리를 바꾼후에 삭제
- 그다음 노드의 자료수는 M/2 이상이어야 하는 원칙에 의해
삭제한 곳의 노드의 자료수가 M/2보다 작다면(underflow) 형제에게 빌리거나,
부모하나와 형제와 결합
- 재배열 필요시 2번 반복
1-1. Leaf Node인 경우
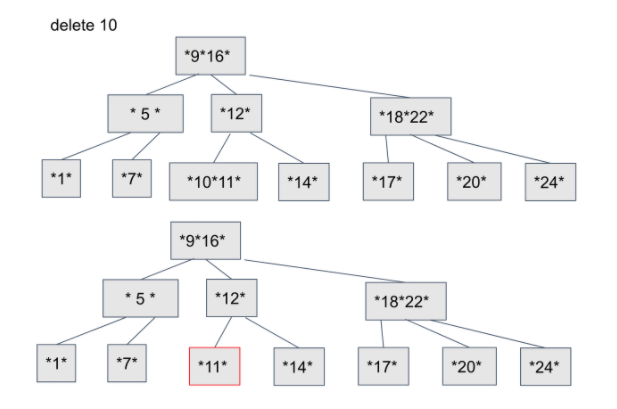
1-2. Leaf Node에서 underflow발생시
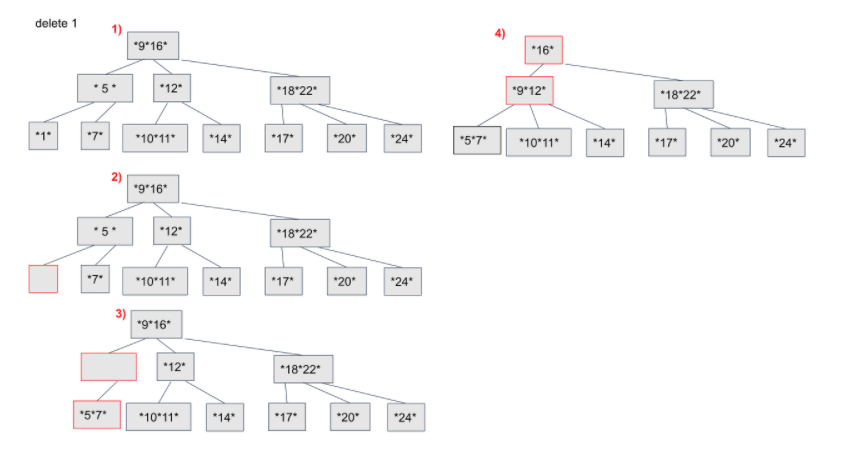
1을 삭제하면 underflow발생하기 때문에 1의 부모와 형제노드를 결합합니다. 이 과정을 조건이 root 로 올라가며 조건이 성립할때 까지 반복합니다.
2-1. Leaf Node가 아닌경우

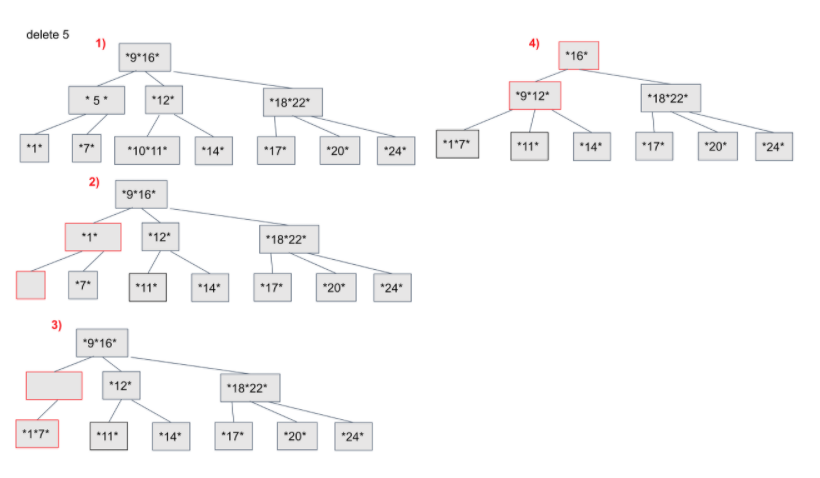
현재 18이 포함된 노드에는 자식이 존재합니다. 이때 18의 왼쪽 서브트리의 가장 큰 데이터와 18을 교체합니다. 그리고 Leef Node가 된 18을 삭제합니다. 그리고 이전 상황처럼 부모와 형제의 데이터를 결합하여 가져오는 과정을 반복합니다.
2-2 Leaf Node가 아닌 경우
B-Tree 장단점
- 장점 : 노드의 삽입, 삭제후에도 균형 트리 유지로 균등한 응답속도 보장 시간 복잡도 : O(logN)
- 단점
- 삽입과 삭제시 트리의 균형을 유지하기 위해 복잡한 연산이 필요
- 메모리 낭비 → 노드가 많아질수록 전체 노드의 상당수가 비게되어 메모리 낭비가 발생 ( 1/2일때 분열이 일어남, 2/3일때 분열이 되는 B*Tree 활용)
- 순차탐색시에는 중위 순회로 비효율적임 → B+ 트리 사용
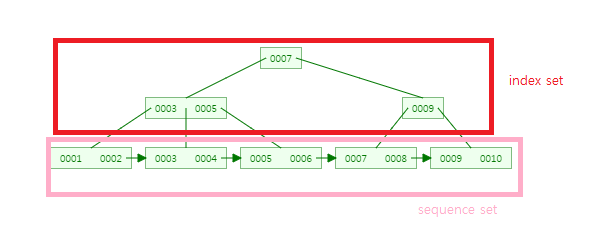
B+트리
- Index node들과 Data node로 구성
- Index node : 리프노드를 제외한 나머지 노드
- Index set : index node 들의 모임 → 데이터의 빠른 접근을 위한 인덱스 역할
- Data node : 리프노드
- sequence set : 리프노드의 모임 → 오름차순으로 정렬( 실제 데이터)
- Data node 는 연결리스트로 형성되어 있다.
- B트리의 순차접근에 대한 문제의 해결책으로 제시되었다.
- B트리와 다르게 삽입, 삭제연산이 리프노드에서만 이루어진다.
- 장점 : B+트리의 높이는 B트리보다 낮게 구성되므로 검색시간과 디스크 접근횟수가 줄어든다.
- 단점 : B Tree의 경우 best case에는 루트에서 끝날수 있지만, B+ Tree의 경우 무조껀 leaf노드까지 가야한다
B+트리의 삽입
- B트리와 유사하며, 리프에 오버플로우가 발생하면 두개의 노드로 분할하고 키 값들을 절반씩 분배해서 저장
- 차수가 홀수일 때, 분할되서 부모로 올리는 값은 t-1번째 값 (t= M/2
- 차수가 짝수일 때, 분할되서 부모로 올리는 값은 t번째 값
- https://www.cs.usfca.edu/~galles/visualization/BPlusTree.html
- B+트리의 삭제연산은 리프노드에서만 실행되기 때문에 단순
- 키 값을 삭제했을 때 리프노드가 underflow되지 않으면 키값을 삭제하고 index set에서도 삭제 후 적절한 key 값을 그 자리에 넣는다.
- 키 값을 삭제 했을 대 리프노드가 underflow가 되면 형제노드에게 값을 빌리거나 병합한다

- → t -1 = (3/2)의 올림수 -1 = 1 이므로 1번째 값인 3이 다시 부모인덱스로 간다.
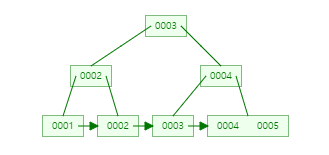
- → t -1 = (3/2)의 올림수 -1 = 1 이므로 1번째 값인 4가 부모 인덱스로 올라간다.
- (5)삽입
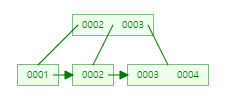
- → t -1 = (3/2)의 올림수 -1 = 1 이므로 1번째 값인 2가 부모 인덱스로 올라간다.
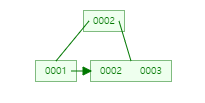
- (3)삽입
- (1,2) 삽입
(2)삭제
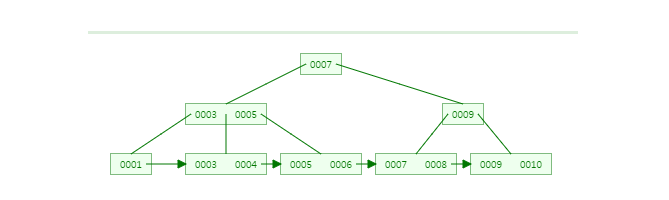
→underflow 없기 때문에 그냥 삭제
(1) 삭제

→underflow 발생하면 형제노드 (3,4)확인 → 빌릴 수 있기 때문에 3을 1 이 있던 노드에 빌려준다.
→index노드에서 3을 삭제하고 4로 대체한다.
(3)삭제

→underflow발생 → 형제노드(4)확인 → 못빌림 → 병합
B트리 VS B+트리
공통점
- 모든 leaf의 depth가 같다
- 각 node에는 k/2 ~ k 개의 item이 들어있어야 한다.
- add시 overflow가 발생하면 분할한다
- delete 시 underflow가 발생하면 형제노드에서 빌리거나 합병 한다.
차이점
- B-tree의 각 노드에서는 key 뿐만 아니라 data도 들어갈 수 있다한다.
- -B+tree는 각 node에서는 key만 들어가야 한다. 그러므로 B+tree에서는 data는 오직 leaf에만 존재
- B+tree는 B-tree와는 달리 add, delete가 leaf에서만 이루어진다.
- B+ tree는 leaf node 끼리 linked list로 연결되어 있다.
B* 트리
- B 트리는 구조를 유지하기 위해 추가적인 연산이 필요(재분배 , 합병 , 분열)
- B*트리는 이러한 문제를 보안하기 위해 나왔으며 B트리에서 최소 2/M의 키값을 가져야한다는 것은 2/3의 키값을 가져야한다고 변경함(메모리 효율)
- 리프를 제외한 모든 노드는 m개의 서브트리 이상을 가질 수 없다
- 루트와 리프를 제외한 모든 노드는 적어도 [(2m-2)/3]+1개의 서브트리를 갖는다.
- 루트는 리프가 아닌 이상 최소 2개, 적어도 2[(2m-2)/3]+1개의 서브트리를 갖는다.
- 모든 리프는 같은 레벨에 있다.
- 리프가 아닌 노드의 키 값의 수는 그 노드의 서브트리수보다 하나 적다
- 각 리프노드는 최소[ (2m-2)/3]개, 최대 m-1개의 키 값을 갖는다.
'Computer Science (CS)' 카테고리의 다른 글
| [Computer Science] 정렬(선택, 버블, 삽입) (0) | 2022.10.10 |
|---|---|
| [Computer Science] 힙(Heap) (0) | 2021.10.14 |
| [Computer Science] 레드블랙트리(Red-Black Tree) (0) | 2021.10.14 |
| [Computer Science] 큐(Queue), 덱(Deck) (0) | 2021.09.13 |
| [Computer Science] 이진트리 (Binary Tree) (0) | 2021.06.28 |



